DETERMINANTE DE MATRIZ QUADRADA
Matriz quadrada é uma matriz que apresenta o número de linhas e colunas iguais. A toda matriz quadrada está associado um número que recebe a denominação de determinante. Os determinantes apresentam aplicações na resolução de sistemas lineares e no cálculo da área de um triângulo no plano cartesiano, quando são conhecidas as coordenadas de seus vértices.
Veremos como se dá o cálculo do determinante de matrizes quadradas de 1ª, 2ª e 3ª ordem
Determinante de uma matriz de 1ª ordem.
Dada uma matriz quadrada de 1ª ordem M = [a11], seu determinante será o número a11. Ou seja:
det M = a11
A = [ 2 ]
Det A = 2
Determinante de uma matriz de 2ª ordem.
Dada uma matriz quadrada de 2ª ordem, seu determinante será obtido fazendo a diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Ou seja:
![]()
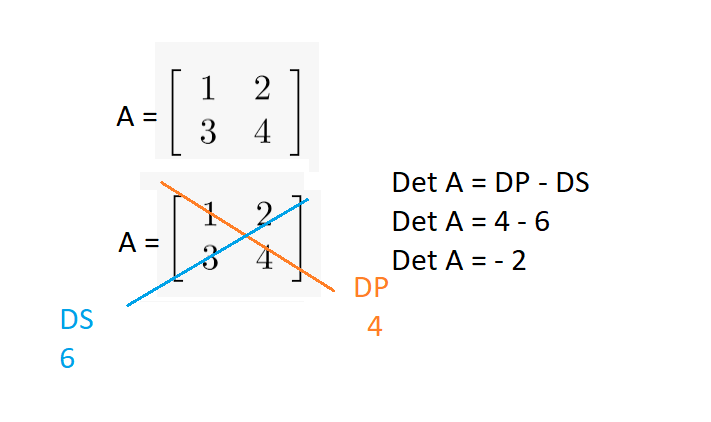
Determinante de uma matriz de 3ª ordem.
Para calcular o determinante de uma matriz quadrada de ordem 3 utilizamos o método de Sarrus. Observe como se dá esse processo:
Considere a matriz quadrada de 3ª ordem a seguir:
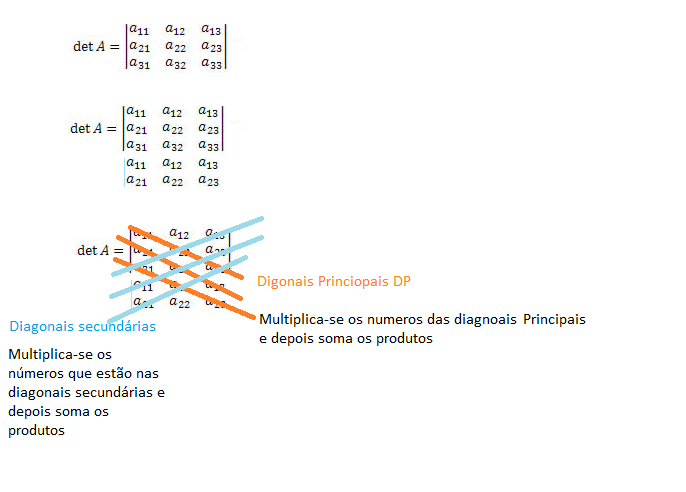
O método de Sarrus consiste nos seguintes passos:
1º: Repetir as duas primeiras linhas , logo abaixo da 3 linha.
2º: Multiplicar os números que estão na Diagonal Principal - DP e somar os produtos
3º Multiplicar os números que estão na Diagonal Secundária - DS e somar os produtos
4º Realizar a operação Det A = DP - DS
Exemplo da Realização do Calculo de Determinante da matriz quadrada do tipo 3x3
Exemplo da Realização do Calculo de Determinante da matriz quadrada do tipo 3x3

Atividade de aprendizagem
Copiar e responder no caderno,
Tirar foto e enviar para o email dinadomi@live.com
Não esqueça de colocar o nome, número e turma
1) Calcular o determinante em cada caso:
a) ![]()
b) 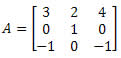
c) A = [ - 5 ]
d)













