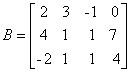Equação Matricial
Continuação dos nossos estudos
- Representação de Equações em uma Matricial
Observe o exemplo:
x + 2 = 4 Trata-se de uma equação, pois:
1º membro: x+ 2
2º membro: =4
Com uma uma variável = X
Quanto temos mais de uma equação e mais de uma variáveis, chamamos de sistema linear
Exemplo:
x + y + z = 20
2x –3y + 5z = 6
4x + 5y – 10z = –3
Podemos transformar este sistema linear em equações Matriciais. veja o exemplo
|
x + y + z = 20 |
x y z b 1 1 1 20 2 -3 5 6 4 5 -10 -3
|
Note que trata-se de 3 equações com as variáveis: x,y e z
e o termo independente "b" que seriam os termos que estão posicionado no 2º membro.
Atividades de Aprendizagem
1) Transforme cada sistema linear em equações matricial. Registre as questões e as respostas em seu caderno.
( Esta atividade vale 2,5 pontos +)
| a) |
2x + 3y = 18 x + 5y = 10 |
| b) |
x - y = 6 4x + 8y = 32 |
| c) |
x + y + z = 9 2x + 2y + 2z = 18 3x + 3y + 3z = 27 |
| d) |
x + z = 4 2y + 3z = 12 x + z = 24 |
2) Acesse o aplicativo a seguir, e realize pelo menos 4 atividades. Registre em seu caderno as questões e as suas respostas.( Esta atividade vale 2,5 pontos +)
Clique na imagem abaixo: Khan Academy , para ter acesso ao aplicativo:
3) Transforme cada equação matricial em um sistema linear . Registre as questões e as respostas em seu caderno.
Mas antes de resolver, pesquise sobre matriz e incompleta
ou pelo site somatemática
( Esta atividade vale 2,5 pontos +)
| a) |
matriz incompleta, pois não tem o termo "b"
|
|
b)
|
Matriz completa, pois tem o termo "b"
|
| c) |
Matriz incompleta, não tem o termo"b" C = ⌈ 2 3⌉ 4 6 |
| d) |
matriz completa , tem o termo "b" |


.jpg)